Now You're Thinking With Needles

This week, I stumbled across the website of Edward S. Lowry, a retired software developer who believes he has created the perfect data structure. He calls this structure the "Needle" (after pine needles), and it looks like this:

In Lowry's system, everything is a needle. Types are needles, entities are needles, relationships are needles, and even integers are needles.

How does this work, and how does it compare to more traditional data structures? I found Lowry's description to be a little confusing, so I'll try my own hand at explaining how it works.

Needle basics #

At its essence, a needle is a collection of 2 pointers:

• A "from" pointer
• A "to" pointer

These pointers can point to other needles, or they can be null.

("Child" and "next" pointers can also be used to make some operations more efficient, but since they are not required, we'll ignore them for now.)

Another way to think about needles is as a series of arrows, where an arrow can branch off of another arrow.

Needle roles #

Ok, so everything is a needle. How do I know what each needle actually represents?

In order to make this work, we need to add additional conventions to distinguish each needle's "role" in the system.

Lowry suggests 3 roles:

• Entity needle - represents an individual entity, an entity class, or a literal value.
• "Peg" needle - represents a collection of entities with a given class. I think of these like a laundry line, where all items hanging from the line are of the same class.
• Link needle - represents a relationship between two entities.

One strange thing about this system is that entities do not contain any information about their own type. Instead, in order to determine the type of an entity, you look at the "peg" needle that the entity is hanging from.

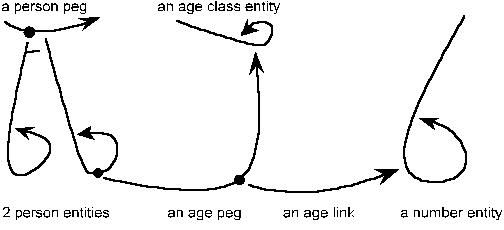
Interpreting the diagram #

So, revisiting the diagram above, we can interpret it as follows:

1. The person peg needle is a collection of person entities. (Presumably this points to a person class entity that is omitted from the diagram.)
2. There are two person entities hanging from the person peg needle.
3. One of the person entities has a peg needle pointing to the age class entity. We can intepret this as saying: "this person has one-or-more ages, which can be found by looking at the children of this needle".
4. The age of the person is represented by an age link hanging from the age peg needle.

(Note: although it may seem like the circles in the diagram represent pegs, they actually represent the "child" pointer of the peg needle, which, again, we will ignore for now.)

It's okay if this is still confusing post-explanation. I personally had to discuss the Lowry's paper with Claude before I had a clear understanding of how it works.

Are needles the future? #

Probably not. Personally, I found this system to be extremely unintuitive, and I don't think it has the simplicity that Lowry claims. The fact that Lowry invented this system in 1970 and it never gained traction is a strong indictment in itself.

However, I do think needles have some interesting properties that make them worth exploring further. In particular, there may be some algorithms that work well with needles that don't work with more traditional data structures. I plan to do more tinkering on my own to determine if this is the case.

(I wouldn't be surprised to find that this structure has already been studied by computer scientists under a different name. If you're aware of any such work, please reach out!)

< Back to all posts